
Diyet, fiziksel olarak sağlığı korumak veya düzeltmek amacıyla uygulanan beslenme düzeni, perhiz ya da rejim olarak tanımlanır. Ruhen ve zihnen de aynı amaca hizmet eden yöntemlerin bütününe de “diyet” adı verilebilir.
Klasik diyet problemi en az parayla sağlıklı bir diyeti organize etme sorusuna cevap arar. Gelin bu probleme bir göz atalım:
“Tanya Smith sporu ciddi bir uğraş olarak görür. Her gün spor salonuna gider, yediğine ve içtiğine de dikkat eder. Sağlıklı ve zinde kalmak için vitamin ve mineralleri her ay doğru miktarlarda alması önemlidir. Bu miktarları ise koçu belirler.
Koçun dediğine göre olimpiyat şampiyonluğu adaylarının vücutlarına her ay en az 120 mg vitamin ve 880 mg mineral alması gerekirmiş. Tanya bu diyete uymak için 2 farklı besin takviyesi alır. Birisi katı haldeki Solido, diğeri sıvı haldeki Liquex. Tanya’nın sorunu koçunun söylediklerini tam olarak yerine getirmek için hangisinden ne kadar alabileceğini hesaplamak.”
Diyet Problemi
Tanya, Solido ve Liquex’in içeriğini inceler. Solido kutusunun üzerinde yazanlara göre içinde 2 mg vitamin 10 mg mineral; Liquex’de ise 3 mg vitamin 50 mg mineral vardır. 30 kutu Solido ve 5 şişe Liquex alır. Sonra hesabını yapar. Aldıklarına göre elinde toplam 75 mg vitamin (2*30=60 ve 3*5=15; 60+15=75); 550 mg mineral (10*30 + 50*5=550) olduğunu görür.
| Solido | Liquex | Gereken Miktar | |
| Vitamin | 2 mg | 3 mg | 120 mg |
| Mineral | 10 mg | 50 mg | 880 mg |
Tanya koçun dediği miktarı düşününce ilaç reyonuna geri dönüp 10 kutu Solido ve 10 şişe Liquex daha almaya karar verir. Yeniden hesap yapınca elinde 125 mg vitamin ve 1150 mg mineral vardır ve koçun isteğinden bile fazla vitamin ve minerale sahip olduğunu düşünür.
İlk aldığı 30 kutu Solido ve 5 şişe (30,5) Liquex kendisine yetmez. Elindeki 40 kutu Solido ve 15 şişe Liquex (40,15) kendine yeterli gelir.
Ama problemin olası birden çok çözümü mevcuttur. Nasıl mı?
İsterse sadece 88 kutu Solido alır (88,0).
(2*88 + 3*0= 176 mg vitamin; 10*88 + 50*0=880 mg mineral)
Ya da sadece 40 şişe Liquex alır (0,40).
(2*0 + 3*40=120 mg vitamin; 10*0 + 50*40=2000 mg mineral).
Görüldüğü gibi bu miktarlar koçun dediği miktarları karşılar. Asıl soru şurada başlar, peki olasılıkların içerisine harcanacak parayı optimize etme sorunu girerse uygun çözüm hangisi olur?
İlaçların her ikisinin de fiyatları 5 dolardır. Dolayısıyla çözüm olarak bulunan (40,15), (88,0) ve (0,40) değerlerinin maliyetleri sırasıyla 275, 440 ve 200 dolardır. Basit matematik hesabıyla (0,40) olan değer yani hiç Solido almayıp 40 şişe Liquex almak en uygun sonuç gibi görünmektedir.
Ya daha farklı bir çözüm söz konusu ise? Tanya da bu soruyu sorar ve doğrusal programlama konusunun mantığını düşünür.
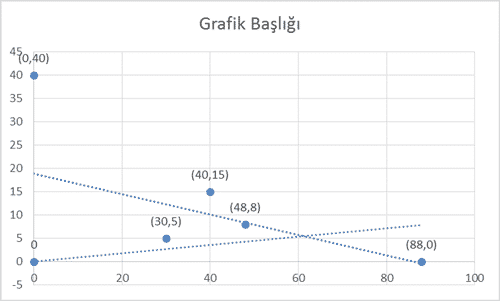
Tanya grafiğe baktığında (48,8) noktasında yeni bir çözüm keşfeder. Yani 48 kutu Solido ve 8 şişe Liquex almayı koçun isteğini tam sağlayan (120 mg vitamin ve 880 mg mineral) çözüm olarak düşünür. Fakat bunun maliyeti ise 280 dolardır. Yani ya parayı düşünüp 200 dolara 40 şişe Liquex alabilir ya da miktarı düşünüp 280 dolara 48 kutu Solido ve 8 şişe Liquex alabilir.
Anlaşılacağı gibi optimum çözüm, görece paraya da bağlıdır. Eğer Solido’nun kutusu 2 dolara düşerse ve Liquex 7 dolara çıkarsa (0,40), (48,8) ve (88,0) kombinasyonları için maliyetler sırasıyla 280, 152 ve 176 dolar olur ve en akıllıca seçim bu durumda 48 kutu Solido ve 8 şişe Liquex almaktır. Klasik diyet problemiyle başlayan sorumuz bizi doğrusal programlamanın mantığını anlamaya kadar götürür.
Doğrusal programlamanın tarihçesi.

Fourier 1826 yılında doğrusal programlamayı çağrıştıran çalışmalar yapar; Gauss ise doğrusal denklemleri Gauss eleme yöntemiyle çözer. 1902 yılına gelindiğinde Farkas, eşitsizlik sistemlerinin çözümüne ulaşır.
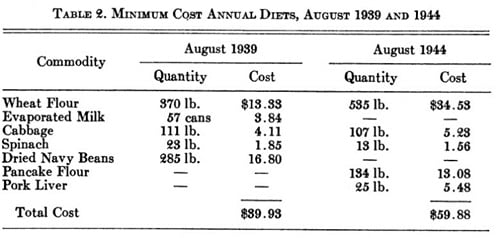
1945’de Stigler diyet problemi için üstünkörü bir yöntem bulur (yukarıdaki görselde örneği vardır). 1947 yılına gelindiğinde ise Amerikalı matematikçi George Dantzig, Amerikan Hava Kuvvetleri adına çalışırken doğrusal programlama problemlerini çözmek için “Simplex Metodu ”nu geliştirir. Bu çalışmasıyla Batıda doğrusal programlamanın babası olarak kabul edilir.
Soğuk Savaş döneminde Sovyet Rusya’da Leonid Kantorovich bağımsız bir doğrusal programlama kuramı bulur. 1975 yılında Kantorovich ve Hollandalı matematikçi Tjalling Koopmans, doğrusal programlama yöntemleri kullanan kaynak dağıtımı konusundaki çalışmaları ile Ekonomi Nobel’ini kazanırlar.
Tanya’nın çözümü iki değişkenli algoritma iken günümüzde artık binlerce değişken içeren problemlerin çözümleri bilgisayarlar aracılığıyla kolaylıkla bulunur.
Oysaki 1938’de 9 vitamin gereksinimli 77 değişkenli bir diyet problemini çözmek için New York’ta 10 kişi 12 gün boyunca hesap yapar.
1984 yılına gelindiğinde Hintli matematikçi Narenda Karmarkar oldukça pratik yeni bir algoritma geliştirir. Rus Leonid Khachiyan ise daha çok kuramsal öneme sahip yeni bir yöntem bulur.
Temel diyet probleminin yanında doğrusal programlama çok değişik alanlarda kendine yer edinir. Nakliye problemlerinden fabrika depolarına mal taşınmasına ya da kâra geçirecek uygulamaları hesaplamada yöntem önemini korur. Yani üretim, finans, pazarlama, reklam ve tarım gibi pek çok alanda maliyetleri minimize edip optimal kaynak dağılımını sağlamak ve karı maksimize etmek için doğrusal programlamadan yararlanılır.
Doğrusal problemlerin temel amacı kârı maksimize edecek optimum çözüme ulaşmaktır. Tanya probleminde ve günümüzde sözün özü ise minimum maliyetle sağlıklı yaşamak!
Kaynakça: Bu yazı Tony Crilly’nin “Gerçekten Bilmeniz Gereken 50 Matematik Fikri” adlı kitabından uyarlanmıştır.
Matematiksel

